Applicazioni del Teorema di Bayes

Il teorema di Bayes è uno strumento potente e versatile che trova applicazione in numerosi campi, dalla medicina alla finanza, dall’informatica all’intelligenza artificiale. La sua capacità di aggiornare le probabilità a priori in base a nuove informazioni lo rende particolarmente utile per la modellazione di situazioni incerte e per la presa di decisioni in contesti complessi.
Applicazioni del Teorema di Bayes in Medicina
Il teorema di Bayes trova ampia applicazione in ambito medico, soprattutto nella diagnostica e nella medicina preventiva.
- Diagnosi di malattie: Il teorema di Bayes può essere utilizzato per calcolare la probabilità che un paziente abbia una specifica malattia, dato un risultato positivo a un test diagnostico. Ad esempio, se un test per il cancro al seno ha una sensibilità del 90% e una specificità del 95%, e un paziente risulta positivo al test, il teorema di Bayes può essere utilizzato per calcolare la probabilità effettiva che il paziente abbia il cancro, tenendo conto della prevalenza della malattia nella popolazione.
- Medicina preventiva: Il teorema di Bayes può essere utilizzato per valutare l’efficacia degli screening medici. Ad esempio, può essere utilizzato per calcolare la probabilità che uno screening per il cancro al colon-retto riduca il rischio di morte per la malattia, tenendo conto della prevalenza del cancro, della sensibilità e della specificità del test, e del tasso di sopravvivenza dopo la diagnosi precoce.
Applicazioni del Teorema di Bayes in Finanza
Il teorema di Bayes trova applicazione in finanza, soprattutto nella gestione del rischio e nella previsione di mercato.
- Gestione del rischio: Il teorema di Bayes può essere utilizzato per calcolare la probabilità di un evento finanziario negativo, come un default su un prestito, dato un insieme di informazioni sul debitore. Ad esempio, un’azienda di credito può utilizzare il teorema di Bayes per valutare il rischio di insolvenza di un cliente, tenendo conto della sua storia creditizia, del suo reddito e del suo patrimonio netto.
- Previsione di mercato: Il teorema di Bayes può essere utilizzato per aggiornare le previsioni di mercato in base a nuove informazioni. Ad esempio, un fondo di investimento può utilizzare il teorema di Bayes per aggiornare la sua previsione sull’andamento di un titolo azionario, tenendo conto dei risultati aziendali recenti, delle tendenze macroeconomiche e di altri fattori rilevanti.
Applicazioni del Teorema di Bayes in Informatica
Il teorema di Bayes trova applicazione in informatica, soprattutto nell’elaborazione del linguaggio naturale, nella visione artificiale e nell’apprendimento automatico.
- Elaborazione del linguaggio naturale: Il teorema di Bayes può essere utilizzato per classificare il testo, ad esempio per identificare lo spam o per categorizzare gli articoli di notizie. Ad esempio, un filtro antispam può utilizzare il teorema di Bayes per classificare un messaggio come spam o come messaggio legittimo, tenendo conto delle parole chiave presenti nel messaggio, del mittente e di altri fattori rilevanti.
- Visione artificiale: Il teorema di Bayes può essere utilizzato per identificare oggetti in immagini o video. Ad esempio, un sistema di riconoscimento facciale può utilizzare il teorema di Bayes per identificare un individuo in un’immagine, tenendo conto delle caratteristiche del viso, della postura e di altri fattori rilevanti.
- Apprendimento automatico: Il teorema di Bayes è alla base di molti algoritmi di apprendimento automatico, come i classificatori bayesiani naif. Questi algoritmi utilizzano il teorema di Bayes per costruire modelli che possono prevedere l’output di un sistema, dato un insieme di input. Ad esempio, un sistema di raccomandazione di film può utilizzare un classificatore bayesiano naif per prevedere quali film un utente potrebbe apprezzare, tenendo conto dei film che ha già visto e valutato.
Applicazioni del Teorema di Bayes in Intelligenza Artificiale
Il teorema di Bayes trova applicazione in intelligenza artificiale, soprattutto nei sistemi di apprendimento automatico e nei sistemi di ragionamento probabilistico.
- Apprendimento automatico: Il teorema di Bayes è alla base di molti algoritmi di apprendimento automatico, come i classificatori bayesiani naif. Questi algoritmi utilizzano il teorema di Bayes per costruire modelli che possono prevedere l’output di un sistema, dato un insieme di input. Ad esempio, un sistema di riconoscimento vocale può utilizzare un classificatore bayesiano naif per prevedere le parole pronunciate da un utente, tenendo conto del suono delle parole e del contesto della conversazione.
- Sistemi di ragionamento probabilistico: Il teorema di Bayes può essere utilizzato per costruire sistemi di ragionamento probabilistico, che possono inferire conclusioni da informazioni incerte. Ad esempio, un sistema di diagnosi medica può utilizzare il teorema di Bayes per inferire la probabilità che un paziente abbia una specifica malattia, dato un insieme di sintomi e di informazioni sul paziente.
Vantaggi e Svantaggi dell’Utilizzo del Teorema di Bayes, Bayesian
Il teorema di Bayes presenta diversi vantaggi, ma anche alcuni svantaggi, a seconda del contesto applicativo.
| Vantaggi | Svantaggi |
|---|---|
| Il teorema di Bayes è un metodo rigoroso e matematico per aggiornare le probabilità a priori in base a nuove informazioni. | Il teorema di Bayes può essere computazionalmente costoso, soprattutto quando si hanno a che fare con un numero elevato di variabili. |
| Il teorema di Bayes è relativamente facile da comprendere e da applicare. | Il teorema di Bayes richiede la conoscenza delle probabilità a priori, che possono essere difficili da ottenere in alcuni casi. |
| Il teorema di Bayes può essere utilizzato per modellare situazioni incerte e per la presa di decisioni in contesti complessi. | Il teorema di Bayes può essere sensibile alla scelta delle probabilità a priori. |
Come il Teorema di Bayes Migliora la Presa di Decisioni e l’Analisi dei Dati
Il teorema di Bayes contribuisce a migliorare la presa di decisioni e l’analisi dei dati fornendo un framework matematico per aggiornare le probabilità a priori in base a nuove informazioni. Ciò consente di prendere decisioni più informate e di analizzare i dati in modo più accurato. Ad esempio, in ambito medico, il teorema di Bayes può aiutare a identificare i pazienti a rischio di sviluppare una specifica malattia, consentendo ai medici di intervenire in anticipo e di migliorare la salute dei pazienti. In ambito finanziario, il teorema di Bayes può aiutare a identificare le opportunità di investimento più promettenti, riducendo il rischio di perdite finanziarie. In generale, il teorema di Bayes fornisce un metodo rigoroso e versatile per l’analisi dei dati e la presa di decisioni in contesti incerti.
Il Teorema di Bayes e l’Inferenza Bayesiana
Il teorema di Bayes, introdotto nel XVIII secolo dal reverendo Thomas Bayes, è un principio fondamentale della probabilità che ha trovato applicazioni in una vasta gamma di campi, dalla statistica all’intelligenza artificiale. Il teorema di Bayes fornisce un modo per aggiornare le nostre credenze sulla probabilità di un evento in base a nuove informazioni o evidenze. L’inferenza Bayesiana, basata sul teorema di Bayes, è un approccio metodologico che ci consente di combinare la nostra conoscenza preesistente (priori) con nuove informazioni (dati) per ottenere una migliore comprensione della realtà.
L’Inferenza Bayesiana e il Teorema di Bayes
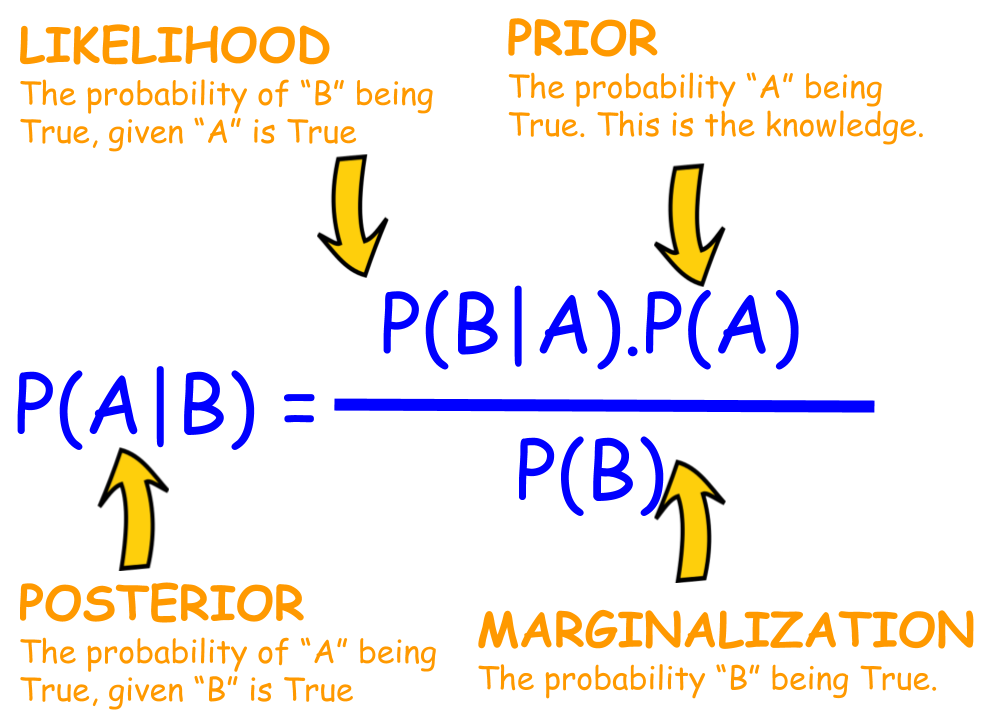
L’inferenza Bayesiana è un approccio alla statistica inferenziale che utilizza il teorema di Bayes per aggiornare le nostre credenze su un parametro sconosciuto in base a dati osservati. In sostanza, l’inferenza Bayesiana ci permette di calcolare la probabilità di un parametro, dato un insieme di dati, utilizzando la probabilità a priori del parametro e la probabilità dei dati condizionata al parametro. Il teorema di Bayes fornisce la formula matematica per questo calcolo:
P(θ|D) = [P(D|θ) * P(θ)] / P(D)
dove:
* P(θ|D) è la probabilità a posteriori del parametro θ, dato l’insieme di dati D.
* P(D|θ) è la probabilità dei dati D, dato il parametro θ (probabilità di verosimiglianza).
* P(θ) è la probabilità a priori del parametro θ.
* P(D) è la probabilità dei dati D (probabilità marginale).
L’inferenza Bayesiana utilizza questo teorema per aggiornare la nostra conoscenza a priori del parametro θ, basandosi sui dati osservati, ottenendo una probabilità a posteriori che riflette le nuove informazioni.
Metodi di Inferenza Bayesiana
Esistono diversi metodi per eseguire l’inferenza Bayesiana, ognuno con i suoi vantaggi e svantaggi. Due dei metodi più comuni sono:
Inferenza Bayesiana di Monte Carlo (MCMC)
L’inferenza Bayesiana di Monte Carlo (MCMC) è un metodo computazionale che utilizza la simulazione per approssimare la distribuzione a posteriori del parametro. Questo metodo si basa sulla generazione di un numero elevato di campioni casuali dalla distribuzione a posteriori, utilizzando algoritmi come l’algoritmo Metropolis-Hastings o l’algoritmo Gibbs. Questi campioni ci permettono di stimare la media, la varianza e altre caratteristiche della distribuzione a posteriori.
Inferenza Bayesiana Variazionale
L’inferenza Bayesiana variazionale è un metodo alternativo che approssima la distribuzione a posteriori utilizzando una funzione di densità di probabilità parametrizzata. Questo metodo cerca di trovare la funzione di densità di probabilità che è la più simile possibile alla distribuzione a posteriori, minimizzando una certa distanza tra le due distribuzioni. La distribuzione variazionale è solitamente più semplice da calcolare rispetto alla distribuzione a posteriori, rendendo questo metodo più efficiente per alcuni problemi.
Sfide e Vantaggi dell’Inferenza Bayesiana
L’inferenza Bayesiana offre numerosi vantaggi rispetto agli approcci tradizionali alla statistica inferenziale, ma presenta anche alcune sfide.
Sfide
* Scelta della probabilità a priori: La scelta della probabilità a priori può influenzare la distribuzione a posteriori. È importante scegliere una probabilità a priori che rifletta la nostra conoscenza preesistente del parametro.
* Calcolo computazionale: L’inferenza Bayesiana può essere computazionalmente costosa, soprattutto per problemi con un numero elevato di parametri.
* Interpretazione dei risultati: L’interpretazione dei risultati dell’inferenza Bayesiana può essere complessa, soprattutto per problemi con distribuzioni a posteriori multimodali.
Vantaggi
* Flessibilità: L’inferenza Bayesiana può essere utilizzata per analizzare una vasta gamma di modelli statistici, inclusi modelli non lineari e modelli con dati mancanti.
* Gestione dell’incertezza: L’inferenza Bayesiana fornisce una misura completa dell’incertezza associata ai parametri, consentendoci di ottenere intervalli di confidenza e probabilità a posteriori.
* Aggiornamento delle credenze: L’inferenza Bayesiana consente di aggiornare le nostre credenze sulla base di nuove informazioni, rendendolo un approccio adattativo all’analisi dei dati.
L’inferenza Bayesiana è un potente strumento per l’analisi dei dati che offre un approccio flessibile e informativo per l’inferenza statistica. Sebbene presenti alcune sfide, i suoi vantaggi la rendono una metodologia sempre più popolare in molti campi, dalla scienza medica all’intelligenza artificiale.
